Verhältnis 3 Zu 1 Berechnen
Verhältnisse berechnen einfach erklärt
Wenn du zwei Zahlen miteinander vergleichen möchtest, kannst du ihr Verhältnis berechnen. Stell dir zum Beispiel vor, du hast 2 Liter Cola und 6 Liter Orangenlimonade für eine Party gekauft. Du willst Spezi mischen. Wie groß ist das Verhältnis von Orangenlimonade zu Cola in deiner Spezi?
Das Verhältnis von Cola zu Limonade ist dice Menge der Cola geteilt durch die Menge an Limonade:
![\[ \frac{ \textrm{Cola} }{ \textrm{Limonade} } = \frac{ 2\,\ell }{ 6\,\ell } \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-7eaeeb4f530cae91fa19ce317cc0d6ef_l3.png "Rendered by QuickLaTeX.com")
Den Bruch kannst du vereinfachen, indem du mit 3 kürzt:
![\[ \frac{ 2\,\ell }{ 6\,\ell } = \frac{ 1 \cdot \cancel{2\,\ell} }{ 3 \cdot \cancel{2\,\ell} } = \frac{1}{3} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-5dcdc0400d51b2a9179715714e80ff26_l3.png "Rendered by QuickLaTeX.com")
Deine Spezi hat ein Verhältnis von Cola zu Limonade von 1 zu iii. In deiner Spezi ist too 3-mal mehr Limonade als Cola. Verhältnisse gibt es nicht nur in Mathe. Häufig musst du beim Kochen und Backen von verschiedenen Zutaten das Verhältnis berechnen.
Verhältnisse bilden
Das Verhältnis von zwei Zahlen 
und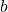 
kannst du benutzen, um und 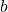miteinander zu vergleichen. Am einfachsten tust du das, indem du die beiden Zahlen durch einander teilst. Das Verhältnis von und 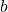ist also:
![\[ \textrm{Verhältnis $\mathit{a}$ zu $\mathit{b}$} = \frac{a}{b} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-0199d464bd62c256131a8b7d4368cf8b_l3.png "Rendered by QuickLaTeX.com")
Dice Reihenfolge ist wichtig! Da musst du aufpassen. Umgekehrt ist das Verhältnis von 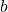und :
![\[ \textrm{Verhältnis $\mathit{b}$ zu $\mathit{a}$} = \frac{b}{a} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-b566bbce5082a0375cdf214b75297e9d_l3.png "Rendered by QuickLaTeX.com")
und 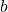heißen Glieder des Verhältnisses. Es gibt viele verschiedene Schreibweisen für Verhältnisse. Lass dich dadurch aber nicht aus der Ruhe bringen! Alle Schreibweisen heißen dasselbe und meinen einen Bruch. Wenn du nicht mehr weißt, wie die Bruchrechnung funktioniert, schau dir dieses Video an.
Verschiedene Schreibweisen erklärt
Du kannst das Verhältnis zwischen 1 und 4 auf verschiedene Weise schreiben:
– als Bruch: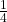 
– mit Doppelpunkt: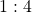 
– mit Querstrich: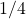 
oder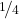 
– mit Worten: 1 zu 4
Verhältnisse berechnen
Folgende Beispiele helfen dir, die Verhältnisrechnung zu verstehen und zeigen dir, wie du die Verhältnisse bildest. Um Verhältnisse zu berechnen, brauchst du häufig die Primfaktorzerlegung und Bruchrechnung. Falls du da nicht mehr and so fit bist, ist das nicht schlimm! Schau dir einfach unsere Beiträge zur Primfaktorzerlegung und Bruchrechnung an.
Verhältnisse in Textaufgaben
Es gibt viele verschiedene Sätze, hinter denen sich Verhältnisrechnungen verstecken können. Wenn du eines dieser Wörter in einer Textaufgabe siehst, musst du die Zahlen ins Verhältnis setzen.
– … das Verhältnis zwischen 1 und 5 …
– … auf one Sachen kommen iii Dinge …
– … 2 Sachen pro 3 Dinge …
– … für i Sache gibt es iv Dinge …
– … ane zu ii …
Verhältnis ausrechnen
Stell dir vor, du hast zwei Zahlen gegeben und sollst das Verhältnis der beiden Zahlen berechnen. Diese zwei Beispiele helfen dir dabei:
Beispiel 1: Seitenverhältnis berechnen
![\[ \frac{a}{b} = \frac{ 48\,\textrm{cm} }{ 27\,\textrm{cm} } \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-16c5a63916a6548d684c5b0afbaed5a4_l3.png "Rendered by QuickLaTeX.com")
- Als Nächstes musst du den Bruch kürzen. Du suchst die größte Zahl, die 48 und 27 teilen kann. Schau dir das Video zum größten gemeinsamen Teiler an, wenn du nicht mehr weißt, wie das geht. 48 und 27 sind beides Vielfache von 3. Die 3 kürzt sich raus:
![\[ \frac{ 48\,\textrm{cm} }{ 27\,\textrm{cm} } = \frac{ 16 \cdot \cancel{ 3\,\textrm{cm} } }{ 9 \cdot \cancel{ 3\,\textrm{cm} } } = \frac{16}{9} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-7e2bd3b72803914111f857d09b5619df_l3.png "Rendered by QuickLaTeX.com")
- Dein Fernseher hat also ein Seitenverhältnis von 16 zu 9.
Beispiel 2: Verhältnisberechnung beim Kuchenbacken
![\[ \frac{ 50\,\textrm{m}\ell }{ 200\,\textrm{m}\ell } = \frac{ 1 \cdot \cancel{50\,\textrm{m}\ell} }{ 4 \cdot \cancel{50\,\textrm{m}\ell} } = \frac{ 1 }{ 4 } \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d19f03c804001291450f2afa698f4b27_l3.png "Rendered by QuickLaTeX.com")
- Dein Kuchen hat also ein Butter-zu-Wasser-Verhältnis von 1 zu four.
Verhältnisglieder ausrechnen Typ i
Eine andere typische Aufgabe ist folgendes: Du weißt das Verhältnis von zwei Dingen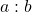 
und du weißt die Gesamtanzahl aller Dinge, likewise 
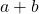. Wie groß sind dann deine Zahlen und 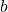?Diese zwei Beispiele 
erklären es dir:
Beispiel iii: Verhältnis berechnen Mädchen zu Jungen
- Stell dir vor, in deiner Klasse sind 20 Schüler und du weißt das Verhältnis von Jungen zu Mädchen ist 1 zu three. In der Schulaufgabe könnte dice Frage lauten: Wie viele Mädchen sind in der Klasse?
- Weil in deiner Klasse das Verhältnis von Jungen zu Mädchen ane zu three ist, besteht sie aus 1 Gruppe Jungen und 3 Gruppen Mädchen. Du kannst deine Klasse in insgesamt 4 Gruppen aufteilen.
- Jetzt verteilst du die xx Schüler auf iv Gruppen, indem du xx durch 4 dividierst und vereinfachst:
![\[ \frac{20\,\textrm{Schüler}}{4} = \frac{ 5\,\textrm{Schüler} \cdot \cancel{4} }{ 1\cdot \cancel{4} } = \frac{5\,\textrm{Schüler}}{1} = 5\,\textrm{Schüler} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-3b74c3f6ad1414bf74de509e09c3c2c3_l3.png "Rendered by QuickLaTeX.com")
- Jede Gruppe besteht also aus 5 Schülern. Das bedeutet 1 Teil deiner Klasse sind 5 Schüler.
- Das Verhältnis von 1 zu 3 sagt dir, dass 3 Teile deiner Klasse Mädchen sind. Es müssen also so viele Schüler deiner Klasse Mädchen sein:
![\[ 3 \cdot 1\,\textrm{Teil} = 3 \cdot 5\,\textrm{Schüler} = 15\,\textrm{Schüler} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-ccf665dac92a08adbec7885f9e246e23_l3.png "Rendered by QuickLaTeX.com")
- Bei einem Jungen-Mädchen-Verhältnis von 1 zu 3 sind von den 20 Schülern likewise xv Mädchen.
Beispiel 4: Verhältnis berechnen in Prozent
![\[ \frac{ 15 }{ 20} \cdot 5 = \frac{15 \cdot 5}{20 \cdot 5} = \frac{15 \cdot 5}{100} = \frac{75}{100} = 75\,\% \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-147f92455fe21b7e4a6ee040dbc608a3_l3.png "Rendered by QuickLaTeX.com")
Verhältnisglied ausrechnen Typ 2
Eine weitere typische Aufgabe gibt dir ein Verhältnis von zwei Dingen 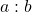und die Menge eines der beiden Dinge . Wie viele gibt es dann von der zweiten Sache 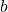? Folgende Beispiele zeigen es dir:
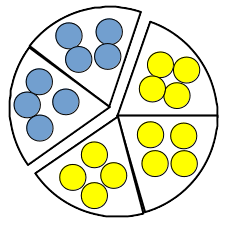
Beispiel five: Murmelsäckchen
- Stell dir vor, du hast ein Säckchen mit Murmeln. Auf der Packung steht: „Für zwei blaue Murmeln sind drei gelbe Murmeln enthalten." Du hast die gelben Murmeln gezählt und weißt, es sind 12 gelbe Murmeln. Wie viele blaue Murmeln hast du?
- Du weißt das Verhältnis von blauen zu gelben Murmeln ist die Anzahl der blauen durch die Anzahl der gelben Murmeln:
![\[ \textrm{Verhältnis von $\mathit{blau}$ zu $\mathit{gelb}$} = \frac{ 2\,\textrm{blaue Murmeln} }{ 3\,\textrm{gelbe Murmeln} } \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d23b02a71024fecc5359485c9119c8d6_l3.png "Rendered by QuickLaTeX.com")
- Dann kannst du das Verhältnis von blauen zu gelben Murmeln mal die Anzahl der gelben Murmeln nehmen, um die Zahl der blauen Murmeln auszurechnen:
![\[ \frac{ 2\,\textrm{blaue Murmeln} }{ 3\,\textrm{gelbe Murmeln} } \cdot 12\,\textrm{gelbe Murmeln} = \frac{ 2\,\textrm{blaue Murmeln} \cdot 12\,\textrm{gelbe Murmeln} }{ 3\,\textrm{gelbe Murmeln} } \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-c327e907b21bdb58569425cdb8d61bb1_l3.png "Rendered by QuickLaTeX.com")
- Den Bruch kannst du wieder kürzen. 12 ist ein Vielfaches von iii:
![\[ \frac{ 2\,\textrm{blaue Murmeln} \cdot 12\,\textrm{gelbe Murmeln} }{ 3\,\textrm{gelbe Murmeln} } = \frac{ 2\,\textrm{blaue Murmeln} \cdot 4 \cdot \cancel{ 3\,\textrm{gelbe Murmeln} } }{ 1\cdot \cancel{3\,\textrm{gelbe Murmeln} } } = \frac{ 2\,\textrm{blaue Murmeln} \cdot 4 }{ 1 } \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-fe1445917f7ba3093431f7bf40802141_l3.png "Rendered by QuickLaTeX.com")
- Anschließend vereinfachst du den Bruch:
![\[ \frac{ 2\,\textrm{blaue Murmeln} \cdot 4 }{ 1 } = 4 \cdot 2\,\textrm{blaue Murmeln} = 8\,\textrm{blaue Murmeln} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-55f827cf8e7ab50ab133ac96166821ab_l3.png "Rendered by QuickLaTeX.com")
- Du siehst: Wenn die Packung 2 blaue für iii gelbe Murmeln enthält und du bereits 12 gelbe Murmeln gezählt hast, müssen 8 blaue Murmeln im Säckchen sein.
Beispiel 6: Verhältnisberechnung Kuchen backen
- Stell dir vor, du willst einen Geburtstagskuchen backen und im Rezept steht „fifty Gramm Mehl reichen für two Personen„, aber es kommen 10 Freunde. Wie viel Mehl brauchst du für den Kuchen?
- Zuerst musst du wissen, wie viel Mehl du für einen Freund brauchst. Teile dafür die Menge an Mehl durch die Zahl der Personen:
![\[ \frac{ 50 \;\textrm{Gramm Mehl} }{ 2 \;\textrm{Freunde} } = \frac{ \cancel{2} \cdot 25 \;\textrm{Gramm Mehl} }{ \cancel{2} \cdot 1 \;\textrm{Freund} } = \frac{ 25 \;\textrm{Gramm Mehl} }{ 1 \;\textrm{Freund} } \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-c267cbc38ecbb68a41d5ba19360bc1e4_l3.png "Rendered by QuickLaTeX.com")
- Das Verhältnis von Mehl zu Freund ist 25 zu i. Rechne das Verhältnis von Mehl zu Personen mal Deine 10 Freunde und vereinfache:
![\[ \frac{ 25 \;\textrm{Gramm Mehl} \cdot 10 \cdot \cancel{1 \;\textrm{Freund}} }{ \cancel{1 \;\textrm{Freund}} } = 10 \cdot 25 \;\textrm{Gramm Mehl} = 250 \;\textrm{Gramm Mehl} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-3bad294dc2bfeaa658481a1266241f75_l3.png "Rendered by QuickLaTeX.com")
- Du musst too 250 Gramm Mehl für 10 Freunde kaufen, wenn das Verhältnis von Mehl zu Freund 25 zu ane ist.
Bruchrechnen
Du hast bestimmt schon gemerkt, dass Brüche beim Verhältnis berechnen das A und O sind. Wenn dich Brüche noch ins Schwitzen bringen, darfst du dir unsere Video zur Bruchrechnung nicht entgehen lassen! Dann läuft dice nächste Schulaufgabe wie am Schnürchen.
Source: https://studyflix.de/mathematik/verhaeltnis-berechnen-2814
Posted by: williamswalwascalith.blogspot.com
0 Response to "Verhältnis 3 Zu 1 Berechnen"
Post a Comment